 Didon achète Carthage par Matthaus Merian l'Ancien
Didon achète Carthage par Matthaus Merian l'Ancien
Chapitre 1 : Introduction (historique) ☝
| 1.1 | Des ancêtres mytiques |
| 1.2 | Sauver l'empire romain |
| 1.3 | Le problème de la traversée |
| 1.4 | Le problème des points de Fermat |
| 1.5 | Des débuts modestes mais glorieux |
| 1.6 | Le problème du régime de Stigler |
La Recherche Opérationnelle! Operational Research en anglais, operation research en américain. Dans les deux cas, l'acronyme est RO. peut être définie comme une aide à la décision qui mobilise tous les domaines des mathématiques et des sciences humaines pour justifier des choix qui finalement seront pris en tenant compte des réalités spécifiques au champ d'application.
Certains affirment que la première trace d'un telle aide à la décision est présente dans le mythe de la fondation de Carthage par la reine Didon au VIIIe siècle avant notre ère. Didon, ayant succédé à son père sur le trône de Tyr phénicienne obligée de fuir la tyrannie de son frère Pygmalion qui a assassiné son mari pour prendre le pouvoir arrive sur la côte de l'actuelle Tunisie et obtient du seigneur local, le roi Jarbas, de prendre possession d'autant de terre qui pourra tenir sous la peau d'un bœuf.
Ayant confiance dans la parole donnée, Didon fit couper en très fines lanières puis assembler cette peau en un long ruban. Elle choisit un site proche de la mer et demanda que l'on délimite une zone circulaire avec la corde en peau de bœuf, parce qu'à périmètre donné, le cercle est la figure géométrique qui enferme la plus grande surface. En fait, l'intuition de Didon, car il s'agissait d'une intuition puisque la démonstration formelle de cette propriété ne fut donnée pour la première fois qu'au XVIIIe par L. Euler* L. Euler, Methodus inveniendi linas curvas maximi minimive proprietate gaudentes sive Solutio Problematis Isoperimetrici Latissimo Sensu Accepti. Springer Science & Business Media, 2007. En fait, si on accepte que la courbe ne soit pas fermée, c'est le demi-cercle qui enclos la plus grande surface, d'où l'intérêt de fonder une ville sur une côte, comme le décida Didon.
 Didon achète Carthage par Matthaus Merian l'Ancien
Didon achète Carthage par Matthaus Merian l'Ancien
En effet, s'il n'est pas possible d'expliquer le pourquoi de la proposition de Didon dans cette introduction, il est aisé de comprendre qu'en réalité ne pas fermer la courbe, c'est augmenter au maximum le périmètre d'un diamètre. Si on définit la Recherche Opérationnelle par des règles, elle correspond aux règles suivantes :
alors il est vraisemblable que le premier analyste à avoir pratiqué la Recherche Opérationnelle fut Archimède qui au IIIe siècle avant notre ère aida infructueusement le roi Hieron II de Syracuse à tenter de repousser l'invasion romaine commandée par Marcellus. En effet, Archimède nous a transmis la méthode qui a gouverné l'approche scientifique qui l'a aidé dans toutes ses inventions comme les catapultes tournées contre les navires des envahisseurs, la vis-sans-fin$\ldots$ : collecte de données, analyse mathématique de ces données et utilisation des résultats pour construire les instruments nécessaires à son objectif.
Mais, certains pensent aussi que sa démarche a été anticipée un siècle et demi plus tôt par Philippe II de Macédoine qui, après avoir étudié l'art militaire sous l'enseignement du fameux Épaminondas de Thèbe, réforma les phalanges grecques imaginées pas son maître sur une base purement mathématique ! La phalange} ou Phalanx (grec ancien) est une colonne de lanciers conçue pour anéantir l'infanterie ennemie lors du choc entre les deux armées.. Plus tard, les romains reprirent le même type de démarche, pour imaginer leurs camps, leurs fameuses tortues et utilisèrent même la psychologie pour les rendre plus efficaces!. Dans une tortue, les soldats témoins d'un prise de panique d'un de leur camarade devaient le tuer immédiatement sous peine d'être eux-même tués par les autres membres de la tortue. Cette menace, dont aucune mise à exécution ne nous est parvenue, suffisait pour maintenir la cohésion du groupe.
Entre 753 avant J.-C. et l'an 200 de notre ère, la Royauté, la République puis l'Empire romain furent continuellement en expansion. Cette expansion ne fut possible que grâce à de très nombreuses légions qui furent le fer de lance de la formation de l'empire. Initialement, c'est-à-dire pendant la république, c'est une armée de citoyens enrôlés selon leur richesse puis selon leur âge. À la fin du Ie siècle avant J.-C., sous le consulat de Marius, elle devient une armée de métier. Chaque légion est censée être composée de 6000 hommes, mais ce nombre fut rarement atteint. Marius exigea aussi que les équipements ne soient plus financés de manière privative, mais par Rome elle-même, mettant en œuvre la première normalisation de l'Histoire.
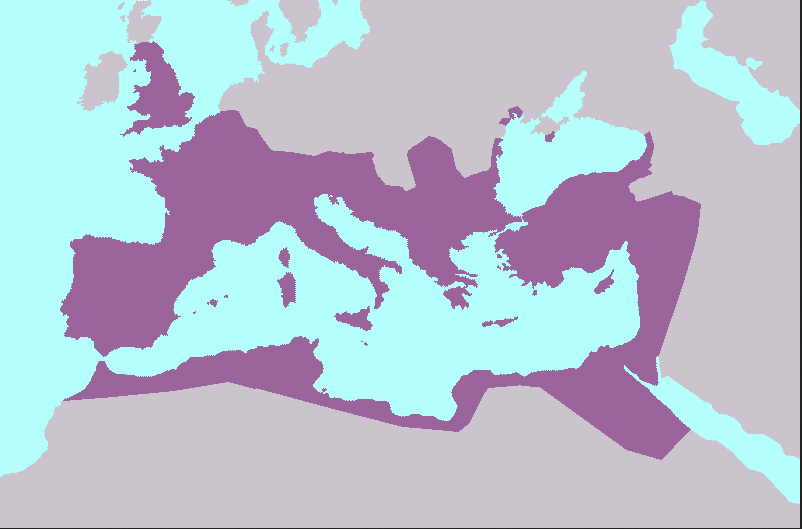
 -510 230 285
Évolution de l'Empire Romain
-510 230 285
Évolution de l'Empire Romain
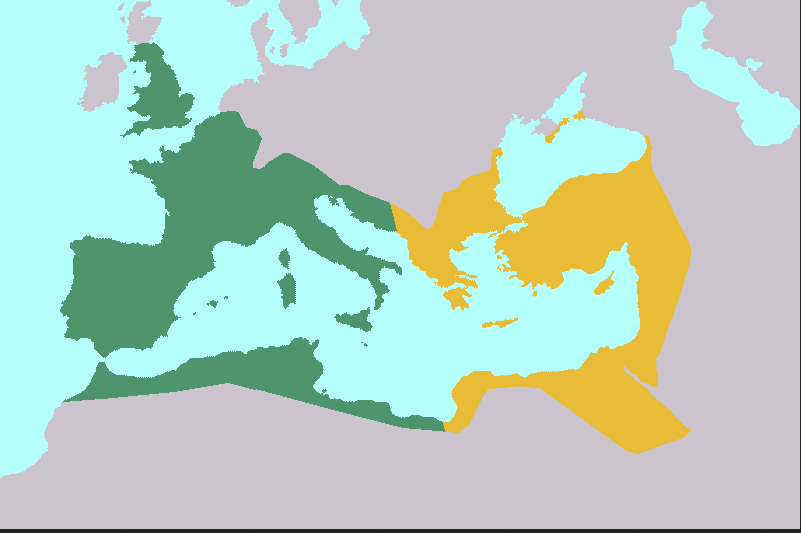
En 230, l'empire atteint son apex mais, très vite, il est assailli par de toutes parts, au point que Doclétien comprend que de part son étendue et la lenteur des transmissions, l'empire ne peut plus être dirigé d'un point central. Il instaure la tétrarchie qui divise l'empire en deux. Cependant, le système était trop complexe pour pouvoir survivre longtemps. En 324, Constantin redevient l'unique auguste des deux empires. Mais, entre temps, la situation s'est véritablement dégradée. Comparés avec les 66 légions qui s'opposèrent à la bataille d'Actium lors de l'affrontement final entre Marc-Antoine et Octave, Constantin ne peut en constituer que 25. Il est devenu impossible de positionner des légions sur tous les points frontière de l'Empire. Constantin construit le plan de défense suivant.
Pour freiner les possibles invasions, il utilise des troupes locales qu'il fera épauler par des armées de champs (approximativement 6 légions épaulées par la cavalerie, l'artillerie et la marine si nécessaire) qui viendront stopper et repousser l'invasion et, si nécessaire, éliminer toute tentative d'insurrection. Par opposition avec la stratégie de défense précédente, qui consistait à empêcher l'entrée quitte à construire un mur physique sur le lieu de la frontière anglo-écossaise! Le fameux mur d'Adrien de 117 km court de la mer d'Irlande à la mer du Nord. Il est flanqué de 300 tours, dont 80 fortins de défense principales et protégé par dix-sept camps retranchés (dixit Wikipedia).} actuelle, la nouvelle stratégie consiste à une défense en profondeur. L'idée est que les milices locales se battant pour leurs propres terres et leurs familles seraient efficaces pour freiner les barbares..
Constantin ne pouvait plus constituer que 4 armées de champs qu'il devait positionner sur son empire décomposé en 8 régions connectées en accord avec le graphe suivant.
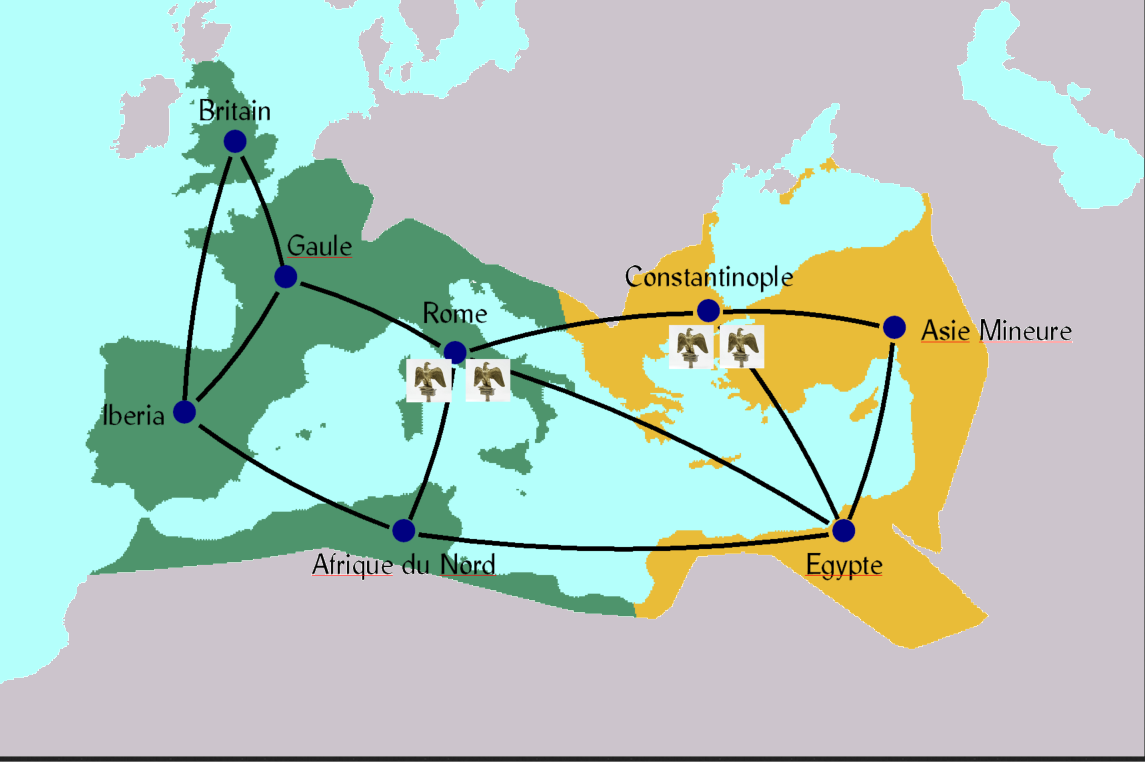 Stratégie de Constantin
Stratégie de Constantin
Le problème que devait donc résoudre Constantin est de protéger les 8 régions, sachant qu'une région est sûre si au moins une armée y stationne et qu'elle est sauvable si elle peut être atteinte par une armée en une étape (sur le graphe, en parcourant un arc et un seul sous la condition suivante qu'elle soit déployée à partir d'une région elle-même sécurisée par la présence d'une autre armée).
Constantin choisit de placer 2 armées à Rome et deux armées dans sa nouvelle capitale, Constantinople. Ainsi, toutes les régions étaient soit sauves soit pouvaient être sauvées en une étape à l'exception de la Grande-Bretagne qui ne pouvait être atteinte qu'en 4 étapes. S'il avait placé une armée en Gaule, deux à Rome et une à Constantinople, la Grande-Bretagne aurait pu être atteinte en deux étapes, mais la situation de l'Asie mineure se serait dégradée puisqu'il aurait fallu deux étapes pour la rejoindre (les autres régions de l'Empire étant soit sauves soit sauvables en une étape). Cette solution est-elle meilleure ? Bien que la pire des situations corresponde à deux étapes contre 4 précédemment, on notera que deux régions sont maintenant dans cette situation. La question posée par ReVelle et Rosing* C. S. ReVelle and K. E. Rosing. "Defendens Imperium Romanum: A Classical Problem in Military Strategy". The American Mathematical Monthly 107, no.7 (2000): 585-594. est de savoir si on peut faire mieux que Constantin. On dispose de plusieurs critères : par exemple, on peut chercher à minimiser le nombre de régions qui ne peuvent être atteintes en une seule étape. Un autre critère consiste à minimiser le nombre d'étapes nécessaire pour relier la région qui est atteinte dans le nombre d'étapes le plus grand.
Ce problème est un véritable problème de Recherche Opérationnelle qui s'est posé à Constantin alors qu'il n'avait aucun instrument à sa disposition pour tenter de le résoudre. C'est même en toute certitude le premier problème qui aurait pu être traité par la programmation linéaire, l'outil central de la recherche opérationnelle.
En 781, Alcuin, alors en charge de l'école de la cathédrale de York, fait un pèlerinage à Rome et, sur le chemin du retour, rencontre Charlemagne à Parme. Malgré son âge (49 ans), il accepte l'invitation de ce dernier à Aix-la-Chapelle, pour y animer l'Académie Palatine, un groupe informel de conseillers de Charlemagne et, surtout, pour prendre la tête de l'École du Palais qu'il dirigera jusqu'à sa mort en 804.
Alcuin est un pédagogue. Dans une lettre à Charlemagne écrite en 800, il mentionne l'envoi de certaines figures arithmétiques subtiles, pour le plaisir. Il n'en fallut pas plus pour qu'un texte non signé, dont la plus ancienne copie date de la fin du IXe siècle lui soit attribué plutôt qu'à Bede le vénérable (672/673-735), qui ne fait mention d'aucun texte de mathématiques plaisantes dans ses écrits. Quoi qu'il en soit, le texte comprend 56 problèmes dont 7 types majeurs apparaissent pour la première fois et 2 qui apparaissent pour la première fois dans le monde occidental (on trouvera une discussion sur l'origine des problèmes ainsi que leur traduction du latin à l'anglais dans Hadley et Singmaster* J. Hadley, , and D. Singmaster. "Problems to sharpen the young". The Mathematical Gazette 475 (1992): 102-126..
Les quatre problèmes de traversés de rivières présentés dans ce recueil font partie des problèmes originaux qui sont le fruit de la pensée de l'auteur et ne sont pas lié à la transmission d'une formulation ancienne. Dans la traduction de Hadley et Singmaster, voici comment se présentent ces quatre problèmes (Ils sont traduits en français à la page Les propositions d’Alcuin ) :
C'est certainement le problème du passage de la rivière par le loup, la chèvre et le chou qui est le plus connu peut-être parce que le plus simple.
 Le loup, la chèvre et le chou
Le loup, la chèvre et le chou
Du IXe siècle au XVIe, seules les mœurs changent la présentation de ces problèmes : les amis et sœurs deviennent maris et femmes C'est ainsi que Nicolas Chuquet le présente vers 1484 dans un livre qui ne sera jamais publié de son vivant! Au XIXe siècle, les rôles seront joués par des missionnaires et des cannibales. (voir Chuquet* N. Chuquet, Le Triparty en la Science des Nombres. Imprimerie des Sciences Mathématiques et Physiques, 1881., Trenchant* J. Trenchant, L'Arithmétique de Jean Trenchant departie en troi livres. Ensemble un petit discours des changes, avec l'art de calculer aux getons<:i>. M. Joves 1561., les Récréations Mathématiques du père Leurochon dans Mydorge* C. Mydorge, Examen du Livre des Recreations Mathematiques et de ses problèmes en Géométrie, Mechanique, Optique & Catoptrique. A. Robinot, 1630. et celles de Bachet* C.-G. Bachet de Méziriac, Problèmes Plaisants & Délectables qui se font par les Nombres. Gauthiers-Villars, 1884. écrites en 1612 (On pourra suivre avec Franci* R. Franci, From China to Paris: 2000 Years Transmission of Mathematical Ideas. Franz Steiner Verlag, 2002. la diffusion de ces problèmes en Europe entre la période d'Alcuin et celle de Tartaglia.).
Dans le même temps, en 1500, Pacioli* L. Pacioli, De Viribus Quantitatis. Aboca Museum, 2009. étend le problème à des bateaux pouvant transporter plus de deux passagers (4 ou 5 couples ne peuvent traverser qu'avec des bateaux de 3 places) pointera que sa solution est erronée (sans changer les conditions 4 couples ne peuvent traverser une rivière(On trouvera la démonstration de cette impossibilité dans Lucas* E. Lucas, Récréations mathématiques. Gauthier-Villars et Fils, 1891.). On doit noter que, paradoxalement, Tartaglia * . Tartaglia, General Trattato di Numeri et Misure. Curtio Troiano, 1556. propose une solution pour la traversée de 4 couples, qui sera déclarée fausse (pour des raisons de cohérence avec la manière dont le problème doit être posé) par Bachet dans ses Problèmes Plaisants de 1612. Une première solution sera proposée par Labosne, l'éditeur de Bachet en 1884. Il suffit que le bâteau puisse transporter 3 personnes(voir Lucas* E. Lucas, Récréations mathématiques. Gauthier-Villars et Fils, 1891.) en donne une solution plus simple que celle de Labosne.}. En suivant cette même voie, Lucas généralise le problème des maris jaloux à $n$ couples et un bateau qui ne peut transporter que $n-1$ individus.
Lucas propose alors la généralisation suivante : des maris en nombre quelconque $n$ se trouvent avec leurs femmes au passage d'une rivière; quel doit être le plus petit nombre $x $ de personnes qu'un bateau peut au plus contenir pour effectuer la traversée sans batelier, avec la condition qu'aucune femme ne demeure dans le bateau ou sur une des rives en compagnie d'un ou de plusieurs hommes, si son mari n'est présent.
Dans son livre de 1891, Lucas raconte qu'en 1879 lors du Congrès de l'Association Française pour l'Avancement des Sciences qui se tenait à Montpellier, un jeune lycéen, Cadet de Fontenay, fut le premier à suggérer que le problème avec 4 couples et un bateau ne pouvant transporter que deux personnes pouvait être réglé s'il existait une île au milieu de la rivière. Généralisé, ce problème devient :
Des maris, en nombre quelconque, se trouvent avec leurs femmes au passage d'une rivière; ils rencontrent un bateau si petit, qu'il ne peut porter plus de deux personnes. De plus, la rivière renferme une île sur laquelle on peut s'arrêter. On demande comment toutes ces personnes passeront la rivière, de telle sorte qu'aucune femme ne demeure, soit sur les deux rives, dans le bateau ou dans l'île, en la compagnie d'un ou de plusieurs hommes, si son mari n'est présent.
Lucas* E. Lucas, .L'arithmétique Amusante. Gauthier-Villars, 1885. rapporte que G. Tarry a donné deux extensions importantes du problème :
Tous ces problèmes ont connus des variations qui sont, pour la plupart apparues au XXe siècle! Au XIXe, Charles Dodgson, plus connu sous le nom de Lewis Caroll envoyait des questions de ce type aux petites actrices qui jouaient au théâtre le rôle d'Alice, en particulier aux sœurs Jessie et Sarah (Sally) Sinclair.. On notera le problème de la traversée d'un pont en une heure qui semble avoir été proposée par S. X. Levmore and E. Early Cook* S. X. Levmore and E. Early Cook. Super Strategies for Puzzles and Games. Doubleday & Company, 1981..
Quatre personnes doivent traverser un pont. Le temps nécessaire pour le traverser est variable selon la personne (5 min pour la première, 10 min pour la seconde, 20 min pour la troisième et 25 min pour la quatrième). Il fait nuit et ils ne disposent que d'une lampe. De plus, on a les contraintes suivantes : le pont ne peut être traversé que par deux personnes à la fois, si l'une d'entre elles est munie d'une lampe torche. La plus rapide doit donc adapter son pas au plus lent. La lampe a une durée de vie d'une heure et le pont est trop long pour que l'on puisse la jeter à ceux qui sont resté de l'autre côté. Comment faire pour traverser la rivière en moins d'une heure ?
Malgré l'intérêt évident de nombreuses générations pour les problèmes de traversée de rivière, ce n'est qu'avec B. L. Schwartz* B. L. Schwartz, An analytic method for the "difficult crossing puzzles". Mathelmatics Magazine, vol 34, N°. 4, pp. 187-193. qu'une première approche analytique permettant de résoudre une large classe de ce type a été initiée. Mais, ce n'est que récemment que R. Böndorfer, M. Grötschel et A. Löbel* R. Borndörfer, , M. Grötschel, and A. Löbel, Charlemagne and his Heritage: 1200 Years of Civilization and Science in Europe. Vol. II: The Mathematical Arts, Brepols Publishers, 1998. ont montré que la solution de ces problèmes pouvaient être abordés par une classe particulière de problèmes linéaires dits en nombres entiers. On pourrait croire à un rendez-vous raté: les problèmes existaient mais pas les instruments pour les résoudre. On doit rajouter à cela que même les auteurs de XIXe siècle ne pouvaient avancer sur le sujet qu'en donnant des solutions à des modèles spécifiques à partir de méthodes qui l'étaient elles-mêmes. Enfin, ces problèmes de transport n'incorporaient aucun aspect pratique : ils ont tous été construit pour aiguiser l'esprit des jeunes Aucun esprit, même le plus puissant de son temps, ne pouvait anticiper ce qu'allait devenir, par la suite, la Recherche Opérationnelle (R.O.).
Dès 1629, Pierre de Fermat met au point le premier usage du calcul différentiel en travaillant sur la méthode des Minimis et Maximis. Mais, comme il ne révèle ses efforts à Robertval qu'en 1636, en général, c'est à cette date que l'on fixe l'apparition du calcul différentiel en Europe (il est notoire qu'il y a eu des antécédents en Inde, voir P. Tannery * P. Tannery (1883). Sur la date des principales découvertes de Fermat. Bulletin des Sciences Mathématiques et Astronomiques, 7(1), 116-128. ). À la même époque voulant montrer la puissance de la méthode qu'il vient d'inventer, il propose le problème suivant à l'intelligence de ses contemporains. Il voulait aussi convaincre ses contemporains qu'il n'existait pas de méthode plus efficace pour résoudre son problème que ce qui allait devenir le calcul différentiel :
Soient $A$, $B$ et $C$ les sommets d'un triangle. Quel point $P$ intérieur au triangle minimise-t-il la somme $\overline{PA}+\overline{PB}+\overline{PC}$ ?
En 1644, (le père) Marin Mersenne, sur la route d'un pèlerinage à Rome, présenta, aux étapes de Bologne puis de Florence le problème de Fermat à Bonaventure Cavalieri, Evangelista Torricelli et Vincenzo Viviani. Torricelli fut le premier à trouver et caractériser ce point qui correspond à la première caractéristique des triangles ignorée des grecs! Contrairement à une idée reçue, le point de Fermat est distinct du barycentre.,! Le mathématicien suisse J. Steiner, dans l'ignorance manifeste des travaux antérieurs consacrés à ce problème, retrouva le point de Fermat. De ce fait, certains auteurs parlent du point de Fermat-Steiner.. Mais, la construction de Torricelli ne caractérisait pas l'optimalité du point de Fermat. Il n'est pas très difficile de donner les conditions qui permettent de situer le point de Fermat! Si tant est que le triangle initial ne possède pas un angle supérieur à 120°..
Pour commencer, il faut se rappeler de la loi des $\cos$, qui est une simple extension du théorème de Pythagore aux triangles qui ne sont pas rectangles.
Donc, pour un triangle de sommets $A$, $B$ et $C$ et d'angles $\alpha$, $\beta$ et $\gamma$ pour $a = |BC|$, $b= |AB$| et $c = |AC|$, en appliquant, la loi des cosinus, on a les trois contraintes :
\[ \begin {cases} c^2 = a^2 + b^2 - 2 ab \cos \alpha\\ b^2 = a^2 + c^2 - 2 bc \cos \beta\\ a^2 = a^2 + c^2 - 2 ac \cos \beta =a^2 + c^2 - 2 ac \cos(2 \pi - \alpha-\beta) \end{cases} \]Cette propriété acquise, pour un triangle de sommets $X$, $Y$ et $Z$, le problème que l'on doit résoudre pour trouver le point de Fermat est, ennotant $\alpha$ l'angle déterminé par les sommets $X$ et $Y$, $\beta$, l'angle déterminé par les sommets $ Y$ et $Z$ (par complétion des angles du triangles, l'angle déterminé par les sommets $X$ et $Z$ est $2 \pi - \alpha - \beta$ :
\[ \begin{array}{c} \min_{\{x, y, z\}}x + y + z\\ \text{\small sous les contraintes}\\ a^2 = x^2\ + y^2 - 2 x y \cos \alpha\\ b^2 = y^2 + z^2 - 2\ y z \cos \beta\\ c^2 = z^2\ + x^2 - 2\ x y \cos(2\ \pi - \alpha- \beta) \end{array} \]Après écriture du lagragien et des équations d'optimalité du premier ordre, il vient deux conditions :
\[ \begin{cases} \sin\alpha= \sin \beta\\ \sin(\alpha+ \beta)=-\sin \beta\\ \end{cases} \]De la première condition, il vient que $\alpha = \beta$. En substituant ce résultat dans la seconde condition, il vient que :
\[ \sin 2 \alpha = - \sin \alpha \hspace{.25cm}\Longrightarrow\hspace{.25cm} 2\sin \alpha\cos \alpha = 0 \hspace{.25cm}\Longrightarrow\hspace{.25cm} 2 \cos \alpha +1 = 0 \hspace{.25cm}\Longrightarrow\hspace{.25cm}\alpha = 120^\circ \]la dernière condition étant imposée par le fait que $0 < \alpha < 180^\circ$. Bien entendu, en présentant son problème, Fermat ne cherchait qu'à montrer que la méthode qu'il venait de découvrir produisait une caractérisation inégalable de l'optimum recherché. Il était à mille lieux de penser que ce petit problème ouvrait la porte aux problèmes de localisation auxquels l'économiste allemand Alfred Weber* A. Weber (1909), Über den Standort der Industrien. J.C.B. Mohr a associé son nom (En réalité, le problème a été présenté pour la première fois par Thomas Simpson* T. Simpson (1750). The Doctrine and Application of Fluxions. J. Nourse.) et qui a de nombreuses applications aussi bien en économie, qu'en informatique ou encore en biologie.
Après ces temps lointains, il faudra attendre le début de l'année 1776 pour que Gaspard Monge révèle aux académiciens français qu'il s'intéressait à un problème pratique dont il aurait bien aimé trouver la solution qu'en définitive il n'obtint jamais, tout spécialement à la date de la publication de son mémoire sur les déblais & remblais (voir G. Monge G* G. Monge (1781). Mémoire sur la théorie des déblais et de remblais. Histoire de l'Académie Royale des Sciences de Paris, avec les Mémoires de Mathématique et de Physique pour la même année, 666-704.). Sous la plume de Cédric Villani, voici comment le problème peut être présenté : un certain nombre de boulangeries doivent livrer un certain nombre de cafés de façon à ce que ces derniers puissent servir le petit café-croissant du matin. Chaque boulangerie a une capacité limitée de production de viennoiserie. Si les boulangeries s'organisent pour une demande nécessairement localisée des cafés comment organiser la distribution ? Qu'est-ce qui est collectivement optimal : que la boulangerie ❶ répartisse sa production entre les cafés ➀ et ➂ ou d'envoyer l'intégralité de sa production à la boulangerie ➃ (voir la figure suivante) ?
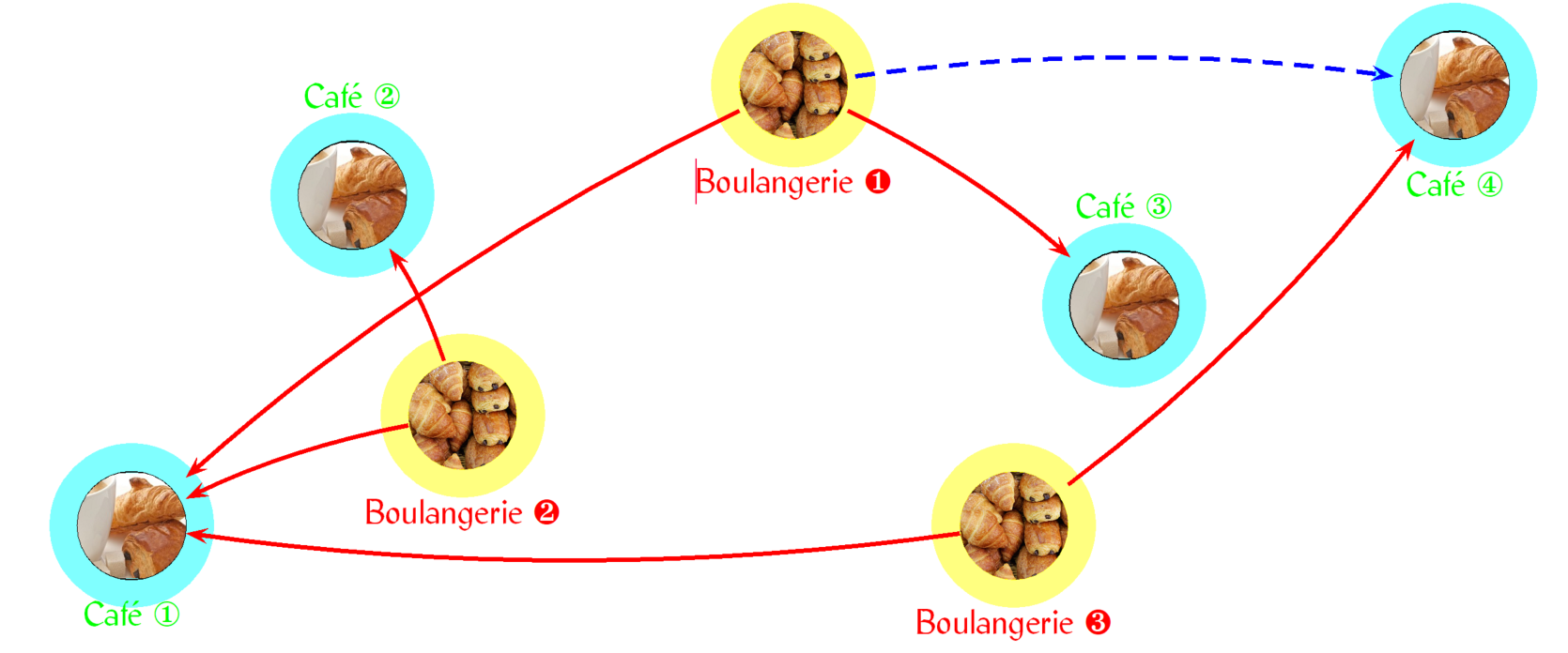 Le problème de Monge (interprétation de Villani)
Le problème de Monge (interprétation de Villani)
Comme le fait remarquer Cédric Villani, Monge était persuadé d'avoir apporté des solutions à son problème alors que dans son mémoire, il obtient des solutions particulières, des algorithmes de calcul pour certaines géométries simples, fait le lien avec des découvertes géométriques remarquables (lignes de courbure des surfaces convexes...), mais ne résout pas le problème général, qui sera d'ailleurs mis à prix par l'Académie des Sciences (voir Le problème du transport).
Il fallut près de deux siècles pour que F. L. Hitchcock* F. L. Hitchcock (1941). The distribution of a product from several sources to numerous localities. Journal of Mathematical Physics, 20, 224-230.. propose la première formulation en termes de programmation linéaire ainsi qu'une méthode de résolution! À sa mort en 1957, le prix Nobel d'économie n'avait pas encore été créé. De ce fait, il n'est apparu que récemment dans les histoires de la programmation linéaire. De plus, l'article de 1941 est son unique contribution au domaine. et, de manière indépendante L. Kantorovich* L. Kantorovich (1942). On the translocation of masses. C.R. (Doklady) Acad. Sci. URSS, 37, 199-201., 20, 224-230. propose une première approche en utilisant les avancées de la géométrie riemannienne et de la théorie de la mesure! Kantorovich a été ignoré et même ostracisé dans son propre pays, parce qu'en inventant la programmation linéaire et en l'appliquant au problème de l'allocation optimale des ressources, ses analyses furent rapidement confrontées au rôle des prix dans l'économie (ce qui était blasphématoire dans la Russie de l'ère soviétique). L'approche suivie par Kantorovitch le conduisit à conclure que les prix sont déterminés par la rareté relative des produits (ce qui n'est autre qu'une forme de réintroduction de la théorie de l'utilité marginale). Comme cette approche s'opposait à la théorie économique marxiste de la valeur travail, qui affirme que le prix d'un produit est déterminé par le travail incorporé directement et indirectement (le capital est du travail accumulé) dans la réalisation de ce produit. En 1971, Kantorovich recevra le prix Nobel en même temps que Tjalling Koopmans..
Si quelques romains furent des cartographes originaux et avertis, allant même au IIIe siècle jusqu'à donner une carte incroyable de l'empire (la carte dite de Peutinger) indiquant non seulement les distances, mais aussi les étapes de ravitaillement entre les villes, les caractéristiques essentielles des lieux, rien n'indique que certains eurent l'idée de calculer la route la plus courte pour se rendre d'un lieu à un autre. Par la suite, vers la fin du IXe siècle, un poète du Cachemire, Rudrata, base un de ses poèmes sur un problème dérivé du jeu d'échec : le tour du cavalier dont la première solution sera donnée vers 840 par le joueur et théoricien des échecs al-Adli ar-Rumi (voir l'animation suivante).
Avant le XVIIIe siècle, un certain nombre de tours du cavalier sont connus. En occident, c'est P. R. de Monmort* P. -R. de Monmort (1713). Essais d'Analyse sur les Jeux de Hasard. Jacques Quillau, Imprimeur-Juré-Libraire de l'Université. qui l'introduit, avant que Léonard Euler, dans une lettre datée du 26 avril 1757 ne s'attaque par des moyens mathématiques à en trouver des solutions.
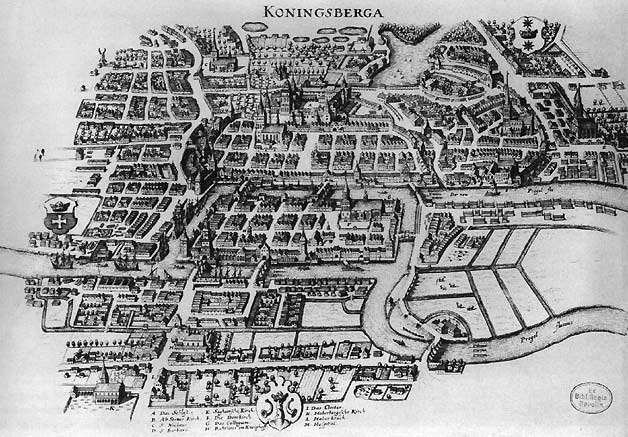 Les 7 ponts de Konigsberg
Les 7 ponts de Konigsberg
Euler n'en était pas à son premier essai en matière de circuits. En effet, dès 1735, le maire de Dantzig lui avait soumis le fameux problème des ponts de Königsberg : peut-on se promener à Königsberg sans passer deux fois sur le même pont et revenir à son point de départ ? De manière très ingénieuse, Euler put répondre par la négative et offrir le premier théorème de topologie de l'histoire des mathématiques (voir Euler* L. Euler (1741). Solutio Problematis ad Geometriam Situs Pertinentis. Commentarii Academiae Scientiarum Imperialis Petropolitanae, 8, 128-140. ).
Si le problème traité par Euler concernait les routes empruntées (on ne peut passer qu'une seule fois par une route reliant deux points), un siècle plus tard, W. R. Hamilton* W. R. Hamilton (1853-7). Account of the Icosian Game. Proceedings or the Royal Irish Academy, 6, 415-416. , empruntant au révérend et mathématicien Thomas Kirkman, redéfinit le problème en imposant un unique passage par chaque sommet. Hamilton, ravis de sa découverte tenta d'en tirer un jeu (the icosian game) qu'il fit éditer sous la suggestion de son ami John Graves qui mit Hamilton en relation avec le fabriquant de jouet londonien John Jacques & Sons. Jacques acquit les droits pour 25 £ et en commercialisa deux versions : l'une comme jeu de plateau et l'autre comme un véritable dodécaèdre. Dans les deux cas, le jeu consistait à relier toutes les capitales des principaux pays du monde à l'aide d'une ficelle. En réalité, le jeu était trop simple même pour des enfants et fut un véritable flop. D'une certaine manière, Hamilton avait construit une méthode permettant d'aborder une des principales difficulté du métier de voyageur de commerce : comment réaliser un circuit ne passant qu'une seule fois par chaque ville visitée avec comme point additionnel de parcourir la distance la plus faible possible.
 The Icosean Game by Hamilton
The Icosean Game by Hamilton
Ce problème avait déjà été traité, certainement par tatonnement, dans le manuel Der Handlungsreisende (wie er sein soll und was er zu thun hat, um Aufträge zu erhalten und eines glücklichen Erfolgs in seinen Geschäften gewiss zu sein) Von einem alten Commis-Voyageur! En traduction libre Le Commis-Voyageur (tel qu'il doit être et ce qu'il doit faire pour recevoir des commissions et s'assurer du succès dans ses affaires)}. Il est amusant de noter que ce mode d'emploi est cité dans le chapitre consacré aux nouvelles publications en Allemagne du {Journal Général de la Littérature de France. de 1833, qui a été porté à la connaissance des chercheurs du domaine par H. MuellerMerbach* H. Müller-Merbach (1983). Zweimal travelling salesman. DGOR-Bulletin, 25, 12-13. . Selon D. L. Applegate, R. E. Bixby, V. Chvá et W. J. Cook * D. L. Applegate, R. E. Bixby, V. Chvátal, & W. J. Cook (2007). The Travelling Salesman Problem. Princeton. , le manuel propose cinq routes à travers l'Allemagne et la Suisse, qui sont des tours (le point de départ est le point d'arrivée). La plus importante d'entre elles, qui passe par 47 villes allemandes est, selon A. Schrijver, certainement optimale étant données les conditions de transport de l'époque.
Il faudra cependant attendre K. Menger* K. Menger (1930). Das botenproblem. (Vol. 2) Teubner. Springer. pour que le problème apparaisse comme un sujet honorable pour mathématiciens. Ironie de l'histoire, Menger voulait introduire une nouvelle définition de la longueur d'une courbe qui manifestement n'a pas fait date. Pour l'appliquer, il retient un problème qu'il baptise le problème du messager (parce qu'il est rencontré par les messagers des postes et d'autres voyageurs) et remarque qu'il est toujours solvable par un nombre fini d'essais, bien que l'on ne connaisse pas encore de règles permettant de les diminuer. En particulier, Menger remarque que la règle consistant d'aller au point le plus proche ne semble pas donner de résultat optimal.
M. M. Flood* M. M. Flood (1956). The traveling-salesman problem. Operation Research, 4, 61-75. rapporte que Albert W. Tucker l'informa que le problème fut amené à la connaissance de la collectivité des mathématiciens américains par Hassler Whitney dans un séminaire de Princeton. On ne peut pas affirmer que Whitney ait lu Menger, mais le problème avait pu germer dans son esprit à partir du circuit fondateur de la littérature universelle, c'est-à-dire le circuit parcouru par Ulysse et qui constitue l'Illiade pour la première étape et l'Odyssée pour le (long) retour. Rappelons qu'il n'y a pas si longtemps, l'Illiade et l'Odyssée faisaient encore partie de l'éducation incontournable de toute personne instruite dans le monde occidentale.
Si on observe la carte représentée à la figure suivante, on constate que le voyage d'Ulysse n'a certainement pas été conçu selon un plan optimal, ce qui n'a rien d'étonnant puisque le tracé de son parcours a été décidé par le courroux de Posséidon.
Mais, il aurait pu aussi être inspiré par les mythes populaires issus de l'histoire de l'Amérique. En effet, pour s'établir en Amérique! Le méthodisme est un courant du protestantisme, qui a été développé par le prédicateur anglais, John Wesley au XVIIIe siècle., l'église méthodique copia et systématisa la méthode du créateur du mouvement qui consistait à parcourir un certain nombre de paroisses éloignées les unes des autres. Comme ils étaient obligés de parcourir leurs circuits à cheval, les prédicateurs méthodistes furent connus sous les noms populaires de coureurs de circuits ou de prédicateurs à sacoches bien que la dénomination officielle fut clergé voyageur.
 Un Cirduit Rider
Un Cirduit Rider
On ne peut affirmer quand l'organisation des circuits pris fin. Mais, ce fut certainement avant la guerre civile. On ne peut aussi affirmer que d'une manière il y eut une tentative d'optimisation des trajets mais le personnage du prédicateur coureur de circuits devint rapidement un personnage mythologique associé au déplacement de la frontière vers l'ouest américain au travers de plusieurs romans célèbres (comme The Circuit Rider d'Edward Eggleston ou The Preacher of Cedar Mountain d'Ernest Thompson) et de bibliographies des prédicateurs eux-mêmes, Peter Cartwright étant connu pour en avoir écrit deux : The Autobiography of Peter Cartwright the Backwoods Preacher (voir P. Cartwright* P. Cartwright (1856). Autobiography of Peter Cartwright The Backwoods Preacher. Cranston & Curts. ) et Fifty Years as a Presiding Elder (voir P. Cartwright* P. Cartwright (1871). Fifty Years as a Presiding Elder. Hitchcock & Walden. ).
Whitney ne pouvait pas ne pas être familier d'une autre source de la mythologie de l'ouest américain, les juges et avocats itinérants qui, à l'image des juges anglais parcourant les districts judiciaires du Royaume-Uni dès le XVe siècle, parcouraient les principaux centres de peuplement des USA. Le plus célèbre de ces juges/avocats fut certainement Abraham Lincoln qui deux fois par ans quittait Springfield (Illinois) et parcourait le Huitième Circuit Judiciaire! Le circuit était essentiellement situé au centre de l'Illinois et était constitué de 14 contés. (voir la figure ci-dessous, empruntée au site! En 1838-1841, le tour passait dans 9 villes.. Lincoln voyageait en tant qu'avocat en compagnie d'autres collègues et d'un juge (le juge David Davis) qui lui demandait de temps à autre de le remplacer. Comme l'arrangement n'était pas légal, Lincoln n'acceptait de siéger à sa place que quand les parties étaient consentantes. Ainsi, le petit groupe apportait la justice au peuple en voyageant à cheval et demeuraient, en général, moins d'une semaine sur place à rendre justice et à plaider. Le voyage durait à peu près deux mois et demi et la distance parcourue entre 650 et 800 km (voir H. C. Whitney* H. C. Whitney (1892). Life on the Circuit with Lincoln. Estes and Lauriat. ).
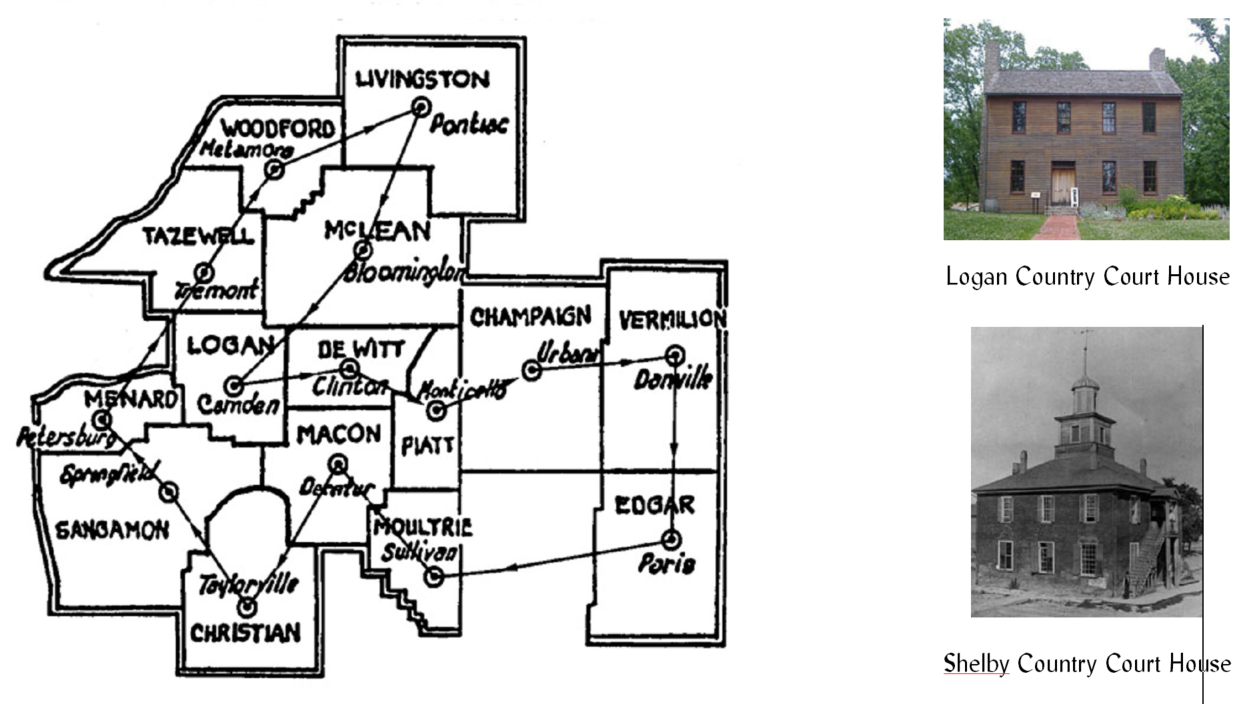 Le circuit de Lincoln
Le circuit de Lincoln
Une autre tradition qui peut aussi expliquer l'émergence du problème repose sur le voyage de formation proposé à la jeunesse aristocratique européenne dès la fin du XVIIe siècle afin d'achever leurs humanités et d'offrir une formation militaire adéquate aux cadets de l'aristocratie. Dès le milieu du XVIIIe siècle l'objet n'est plus le même. Il s'agit plus d'achever l'éducation d'un gentilhomme tant sur le plan social, politique que... sexuel ou d'éloigner un jeune un peu trop turbulent de l'endroit où il doit réaliser plus tard l'essentiel de sa vie. C'est pourquoi l'Italie représentait la destination privilégiée. Parmi les plus célèbres voyageurs qui ont relaté leur Grand Tour, on compte Lord Byron, Gœthe et Alexandre Dumas.
D'une certaine façon, cette tradition fut reprise par Mark Twain dans la seconde moitié du XIXe siècle qui, après s'être embarqué sur le Quaker City, publia le récit de la croisière, dans The Innocents Abroad, qui lui fit faire le tour de la Méditerannée jusqu'en Mer Noire et un voyage en train Marseille-Paris (voir M. Twain* M. Twain (1869). The Innocents Abroad, or The New Pilgrims' Progress. American Publishing Company. ). Si ce voyage eut un immense impact aux USA (il représenta les meilleurs ventes des œuvres du Twain de son vivant et demeure aux USA, l'un des récits de voyage les plus diffusés), il ne fit que populariser l'idée du tour, pas celle de l'optimisation.
Pour revenir au cours de l'histoire, c'est le célèbre statisticien indien P. C. Mahalanobis* P. C. Mahalanobis (1940). A sample survey of the acreage under jute in Bengal. Shankhya, 4, 511-530. qui remet le problème dans l'agenda des chercheurs en montrant que l'un des problèmes les plus importants de la gestion des terres du Bengale est constitué par le problème de transport de la main d'œuvre et des équipements sur leur lieux d'usage. Deux ans plus tard, il semble que R. J. Jessen* R. J. Jessen (1942). Statistical investigation of a sample survey forobtaining farm facts. Research Bulletin, Ames Iowa. traite du même problème, mais il est difficile d'expliquer ce que contient le papier qui est pour l'instant introuvable.
Ce n'est qu'avec J. B. Robinson* J. B. Robinson (1949). On the Hamiltonian game (a traveling-salesman problem). RAND Research Memorandom (RM-303). que le problème va enfin trouver son nom, même si l'introduction du papier est restrictive et qu'il ne montre que la voie à suivre pour tenter de le résoudre Mais, Julia Robinson y reconnaît aussi son échec et propose un algorithme de résolution d'un problème moins difficile : le problème de l'appariement. Avant 1950, on ne peut encore citer que les approximations proposées par E. S. Marks* E. S. Marks (1948). A lower bound for the expected travel among $m$ random points. The Annals of Mathematical Statistics, 19(3), 419-422. eainsi que G. Sierksma et M. N. Gosh49* G. Sierksma & D. Gosh (2010). Networks in Action: Text and Computer Exercices in Network Optimization. Springer Science. .
Si l'on en croît G. Dantzig* G. Dantzig (1990). The diet problem. Interfaces, 20(4), 43-47. , c'est parce que Milton Friedman quitta le Bureau of Labor Statistics en 1937, qu'il eut la chance d'être recruté pour s'occuper des études de consommation des ménages citadins (il n'avait que 23 ans). C'est dans ces locaux qu'il se lia d'amitié avec Duane Evans, qui lui-même collabora avec Wassily Leontieff. C'est ainsi qu'il découvrit les merveilleuses propriétés du modèle Input/Output dont Leontieff s'était fait le champion. Dantzig se rendit tout de suite compte qu'il fallait dynamiser ce modèle et lui associer une fonction objectif. Une fois qu'il eut accepté l'idée que cette fonction objectif pouvait être linéaire, il fallait encore trouver un moyen de le résoudre.
Grâce à la célébrité qu'il avait acquise quelques années plus tôt alors qu'étudiant de Jerzy Neyman il solutionna des problèmes ouverts en statistique (arrivant en retard à un de ses cours et trouvant la salle vide, il avait pris pour des énoncés écrits au tableau pour des exercices! L'anecdote a été reprise en 1997 dans Good Will Hunting de Gus van~Zandt.), il contacta un grand nombre d'économistes et de mathématiciens célèbres, dont Tjalling Koopmans et John von Neumann.
Ne trouvant aucun moyen existant pour résoudre son problème, Dantzig décida d'inventer ses propres instruments. C'est ainsi que naquit l'algorithme du simplexe qui, selon J. L. Casti* J. L. Casti (1996). Five Golden Rules: Great Theorie of 20th Century Mathematics and Why They Matter. John Wiley & Sons. , est un des grands succès des mathématiques du XXe siècle. Il ne restait plus qu'à trouver un sujet pour l'appliquer. Il lui fut suggéré de s'attaquer au problème de la diète qui avait été posé et plus ou moins résolu par Jerry Cornfield en 1941 à la demande de l'armée américaine qui voulait une diète qui pourrait satisfaire les besoins nutritionnels du GI au coût le plus bas possible. Malencontreusement, il s'avéra que Cornfield n'avait pas gardé ses notes, principalement ses données, et comme son étude n'avait pas été publiée, Dantzig se trouva obligé de contacter le Bureau of Home Economics du Département de l'Agriculture. L'interlocutrice avec laquelle il rentra en contact, le renvoya vers G. J. Stigler* G. J. Stigler (1945). The cost of subsistence. Journal of Farm Economics, 27(2), 303-314. qui travaillait sur le même problème que Cornfield.
Dantzig avoue avoir été fasciné par l'article de Stigler qui, pour se protéger des critiques, discute en détail tous les éléments de son modèle. En particulier, quand il parle de pomme s'agit-il d'une Jonathan, d'une McIntosh ou d'une Ontario...? Cette question n'est pas fortuite puisque d'une pomme à l'autre, la teneur en vitamine C peut passer de 4 mg pour 100 g de pommes (pour la Royal Gala) à 30 mg pour 100 g pour la Braeburn! Mais, pour respecter la réalité historique, il n'est pas sur que la et la Royal Gala ait pu être connue à l'époque puisqu'elle a été crée en 1930 en Nouvelle-Zélande et la Braeburn n'est née qu'en 1950..
Il faut dire que l'article de Stigler45 est vraiment étonnant. Il y remarque que l'approche des économistes par la fonction de production qui relie les facteurs de production aux outputs peut être appliquée simplement à la relation entre nutriments et santé. Il remarque qu'il existe des rendements décroissants (une fois passée une certaine quantité minimale de nutriments, toute quantité additionnelle implique un rendement décroissant sur la santé, que la quantité optimale de chaque nutriment dépend des quantités des autres nutriments disponibles).
Par exemple, quand on dépasse la dose optimale d'ingestion de calcium par jour, on accroît pas pour autant son état de santé. Aujourd'hui on sait que cela peut avoir des effets négatifs. On connaît des substances substituables (ou partiellement substituables, comme l'iodine et la thiamine) ou complémentaires (comme la thiamine et la riboflavine).
Toutes les recommandations alimentaires et la nécessité de certains apports peuvent finalement se mettre sous la forme linéaire traditionnelle et représenter la contrainte centrale (par nature, les variables sont nécessairement positives) d'un programme de minimisation du coût.
La méthode adoptée par Stigler pour construire et résoudre son problème est particulièrement intéressante parce qu'elle est à la fois caractéristique de la construction d'un modèle linéaire reflétant les caractéristiques opérationnelles d'un problème pratique, parce qu'elle montre la nécessité du travail de Dantzig et surtout, parce qu'elle offre un bon point de départ pour une analyse critique de cette application.
Le point de départ est la sélection de 77 aliments potentiels dont les prix moyens sur le territoire concerné sont connus (Dans le cas de Stigler45* G. J. Stigler (1945). The cost of subsistence. Journal of Farm Economics, 27(2), 303-314. , les données étaient publiées par le Bureau of Labor Statistics* Bureau of Labor Statistics (1937). Retail Price of Food 1923-1936. Bulletin(635). sous la forme d'une brochure consacrés aux prix de détail.). Stigler note que c'est une restriction et que plus la liste sera grande plus il est vraisemblable que le prix de la diète sera faible. Les denrées alimentaires rassemblées dans cette liste ne comprennent ni fruits frais, ni noix, ni légumes frais bon marché, pas plus que du poisson frais, parce que leur disponibilités et donc leurs prix intègrent entre autre des composantes saisonnières. Même si, à l'époque, la science de la nutrition était encore balbutiante, Stigler pouvait disposer à la fois d'une liste des apports quotidiens que doit consommer un homme d'activité moyenne(Publié par le National Research Counsil* National Research Council (1943/1989). Recommended Dietary Allowances. National Academies Press (US). ) et de la composition des produits naturels dans ces éléments.
Ne disposant que de très faibles moyens de calcul, Stigler adopte la stratégie suivante. Tout d'abord, il exclut tous les aliments dont la valeur nutritive par dollar dépensé est inférieure à celle d'autres aliments. Puis, Stigler élimine les aliments qui sont dominés dans leurs apports en éléments importants par un grand nombre d'autres biens mais qui ne dominent que très faiblement sur certains apports. En opérant ainsi, il passe de 77 biens à 15.
Ayant parfaitement conscience que son problème est un problème linéaire et fort du fait qu'il ne disposait d'aucune méthode pour le résoudre, il construit des aliments composites par combinaison linéaire des autres aliments de telle sorte à ce qu'une combinaison linéaire soit supérieure dans tous les apports à certains biens élémentaires qui peuvent à ce moment être éliminés. De la sorte, il lui reste 9 aliments. En combinant ces 9 aliments restants de manière à ce qu'ils vérifient les conditions requises par une bonne alimentation, il obtient une quantification satisfaisante (mais dont rien ne garantit l'optimalité).
On sait par Dantzig* G. Dantzig (1990). The diet problem. Interfaces, 20(4), 43-47. que pour mettre en œuvre ses calculs, Stigler eut recours à 9 personnes qui utilisèrent ensemble approximativement 120 jours pour arriver à un coût de 39. 69 $ qui s'avéra simplement supérieur de 24 cents au prix optimal (calculé par la suite quand l'algorithme du simplexe fut disponible). Les calculateurs travaillaient chacun séparément (en parallèle) et, quand leurs travaux furent achevés, Stigler les assembla en une large feuille. Impressionnant, isn't it ? D'autant que les diètes à bas prix proposées par les bureaucrates à cette époque coûtaient deux fois plus.
Pour l'anecdote, en 1950, Dantzig déménagea à Santa Monica pour travail pour la RAND Corporation. Ayant accumulé un peu de surcharge pondérale, ses médecins lui conseillèrent une diète pour perdre du poids. Devant ingurgiter moins de 1500 calories par jour, Dantzig se dit immédiatement qu'il risquait d'avoir toujours l'impression d'être sous-alimenté. Un jour, il décida d'adapter le programme de Stigler de telle sorte à ce que les conditions de son régime soient satisfaites tout en ne devant pas subir la sensation d'une faim permanente. Dans son premier essai, qui donnait un panier de consommation assez vraisemblable, l'optimum fut atteint pour un panier exigeant de sa part une consommation de 1892.71l de vinaigre par jour parce que le vinaigre ne contenant pas d'eau, il l'avait classé parmi les aliments qui lui permettraient d'éliminer la sensation de faim. Il élimina donc le vinaigre comme n'étant pas un aliment.
Dans son deuxième essai, il devait consommer 200 bouillon cubes par jour. Il fit l'expérience d'en mélanger 4 dans une coupe : autant manger de la saumure. De ce fait, il appela son médecin pour savoir s'il existait une borne supérieure à la consommation de sel. Ce dernier lui répondit que le corps médical n'y avait jamais pensé dans la mesure où la plupart des gens en bonne santé sont assez censés pour ne pas en consommer trop. Néanmoins, Dantzig imposa une borne supérieure de 3 cubes, créant ainsi la première borne supérieure dans un programme linéaire. Le lendemain, le programme intégrait près d'un kilo de sel. Finalement, sans rejeter pour autant les indications de l'ordinateur, Mme Dantzig pris l'affaire en main et Dantzig perdit 10 kg.